Vanilla options

Option strategies

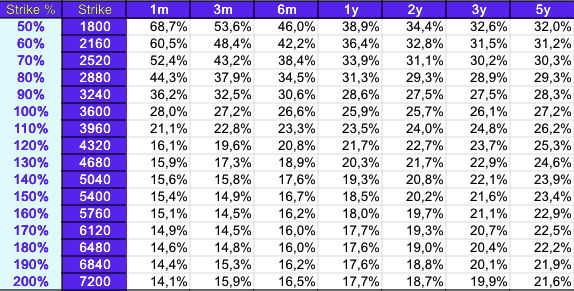
Call fly

The easiest way to find the payoff of a strategy that combines standard calls/puts is to decompose the payoffs as shown below.

Relative value volatility

This strategy is used by hedge funds. It consists in finding arbitrage looking at the volatility curves.

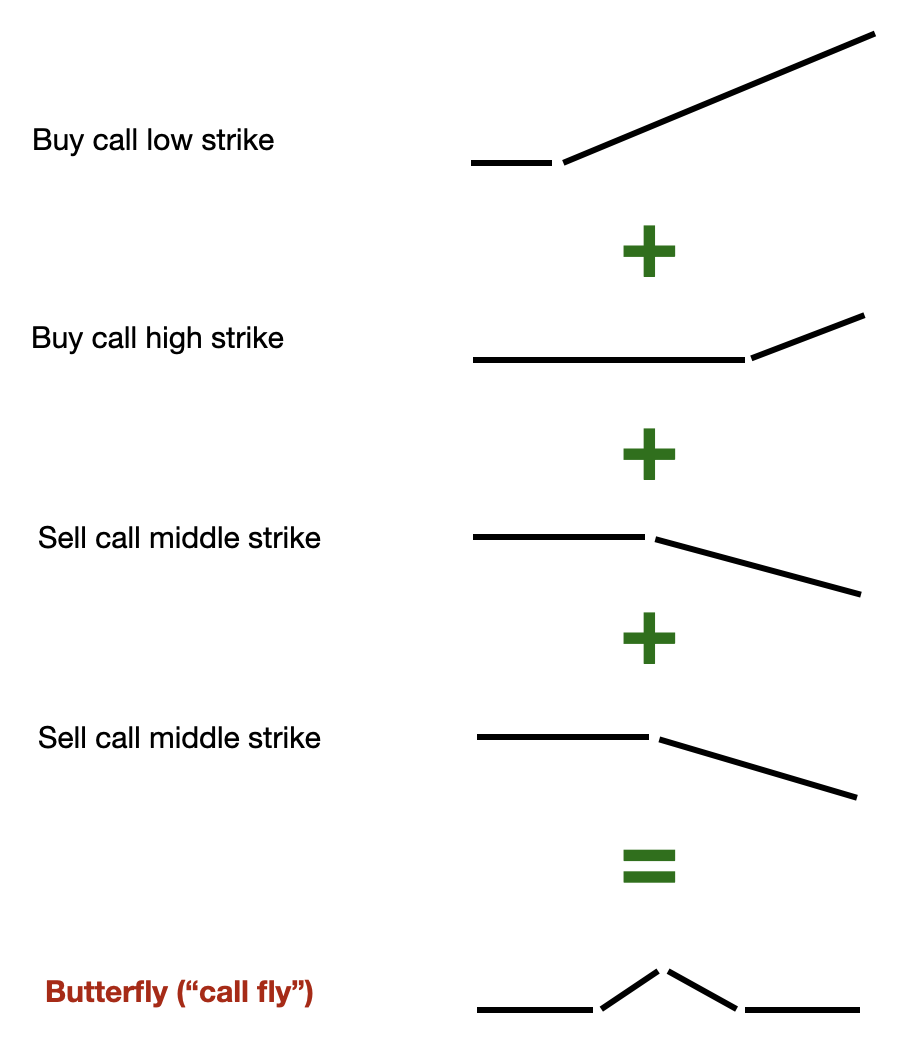
Example 1: look at the spread between 2 options. Say the implied volatility is steep for calls relative to puts:

One possibility would be to sell OTM puts and buy OTM calls hoping that the spread will reduce.

Example 2: in a more sophisticated approach, one can think about looking at relationships between a pool of options.

\[spread = \alpha_0 + \alpha_1 \hat \sigma_1 + \alpha_2 \hat \sigma_2 + ...\]

The positions (long/short) would be taken based on the hope that the spread would revert to historical levels.

Electronic market-making

This strategy is used by hedge funds and rely on making a large number of trades in short times (low latency).

• volatility estimation model to know what are the “fair” implied volatilities to use for pricing -> can be B-S

• interpolation to price illiquid options -> a final volatility surface is obtained

• pricing using B-S or equivalent

• adapt bid/ask spreads depending on volatility and book risk. Example: if a lot of calls (delta positive) have been sold, the book likely has a high delta exposure, thus the HF will lower the ask of puts (delta negative) to make them more attractive and thus reduce the delta.

Note: it can be counterintuitive to use B-S twice (once to get the implied volatility, once to get the price) but it seems that this is often done like so.

Greeks

As showed in the Black-Scholes section,

\[\theta + r S \Delta + \frac{1}{2}S^2\sigma^2 \Gamma = rC\]

Delta

The delta is:

• The sensitivity w.r.t. the underlying move of 1 unit. E.g. Microsoft trades at \$410 and the ATM call is at \$4.7 with a delta of 50%. If the price moves to \$411, the call price becomes 4.7 + 0.5 = \$5.2.

• The estimated probability that the underlying ends up ITM at maturity.

• The quantity of underlying to short to be delta-hedged.

• 50% when ATM. In other words, when buying a call ATM, we earn only half of the underlying’s variation.

When a position is delta-hedged, it can still be profitable on other aspects such as theta (e.g. by selling options and collecting the time decay as time passes) or vega.

\[\Delta_{call} = \mathcal{N}(d_1)\] \[\Delta_{put} = \mathcal{N}(d_1)-1\]

$d_1 = \frac{\ln\frac{S_t}{K}+\left(r+\frac{\sigma^2}{2}\right)\left(T-t\right)}{\sigma\sqrt{T-t}}$

Gamma

The gamma is:

• The sensitivity of the delta w.r.t. the underlying move

Gamma positive: when the underlying increases a lot, the delta increases even more (so the option becomes even more sensitive to the underlying).

Example: when an investor buys a BRC, he is gamma negative (short put). It means that when the underlying decreases (and goes close to the barrier), the delta increases so the option becomes more sensitive to the underlying. Since he is also delta positive, the option would strongly decrease once close to the barrier. That’s why considering selling a structured product when the underlying arrives close to the barrier is not a good strategy.

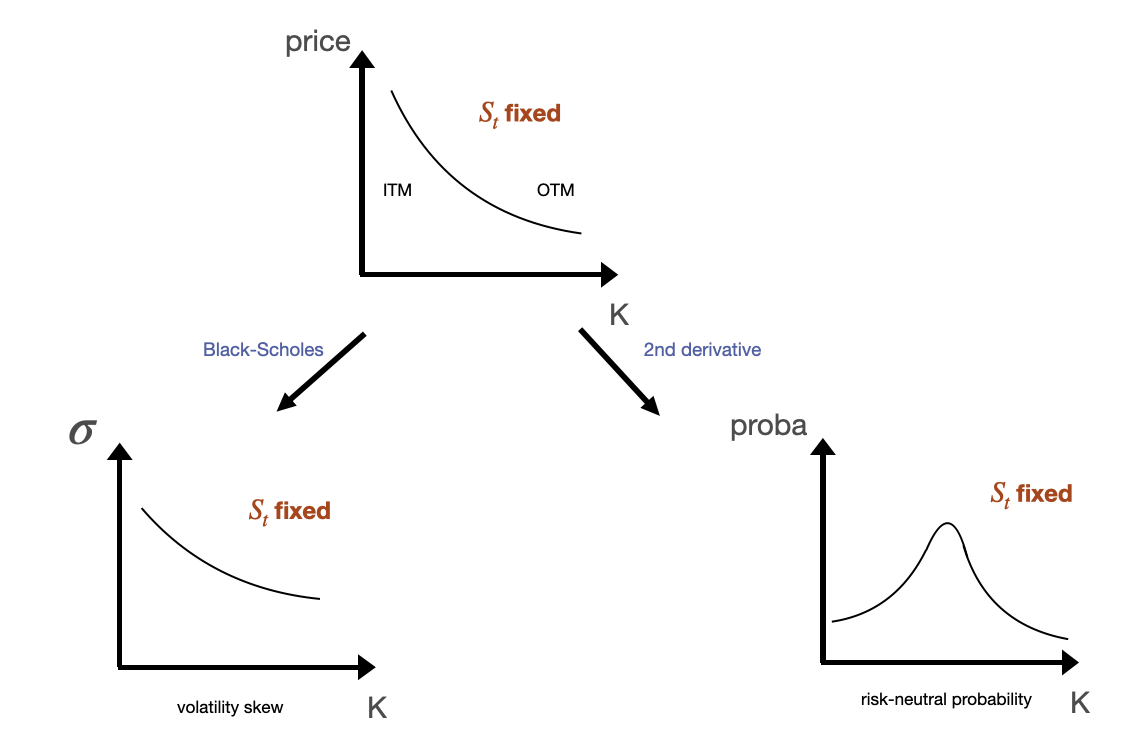
Volatility curves

To price an option, the traders need to know the right implied volatility. Indeed, the implied volatility is the only input that is not observable in the market. In practice, the Black-Scholes model is used to find this implied volatility (rather than to compute option prices). See this tutorial for an example of a volatility curve computation.

Volatility w.r.t the strike

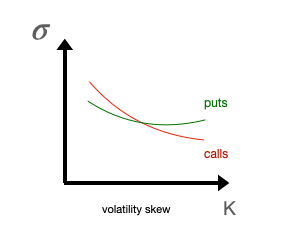
It’s the implied volatility plotted against the strike. For FX options, it has a “smile” shape. For equity options, it has a “skew” shape.

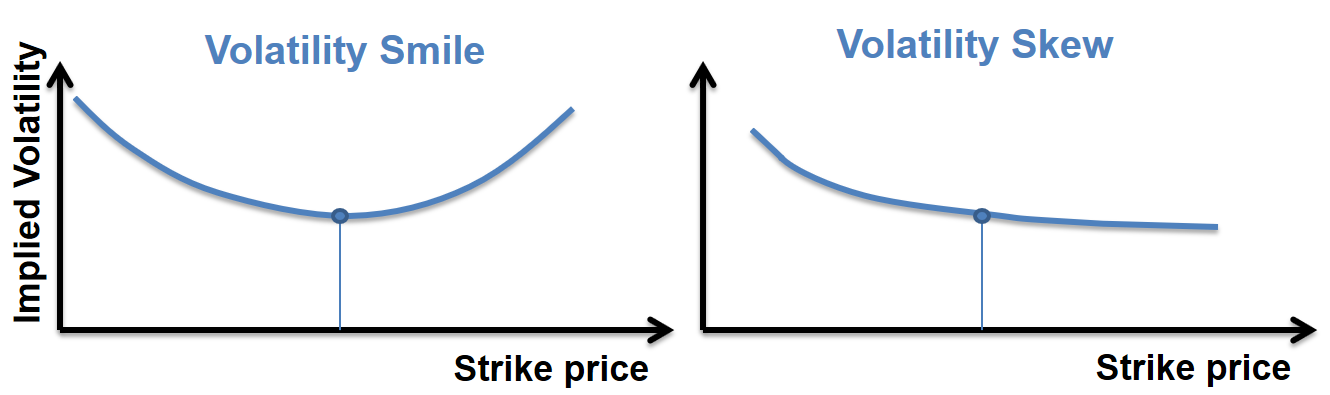
For FX options, the smile can be explained in computing the associated risk-neutral distribution (also called implied distribution):

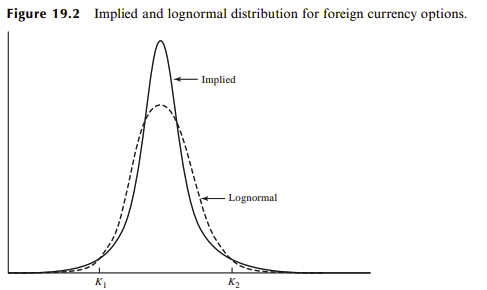
In Black-Scholes model, the assumed risk-neutral distribution is lognormal. As we can see, the “real” risk-neutral probability function deduced from the volatility smile has a larger kurtosis than a normal distribution. That’s because in reality, extreme events happen more often. Since we know that Black-Scholes assumes a constant volatility, the assumed volatility curve is flat. In reality, when an option is DOTM (strike $K_2$ (not $K_1$!) of the above graph), the spot has more chances to get higher than under the B-S assumptions. Hence the DOTM option should be more expensive, so the implied volatility should be higher. Similar reasoning for DITM, hence the smile.

For equity options, the skew can be explained similarly in computing the risk-neutral distribution:

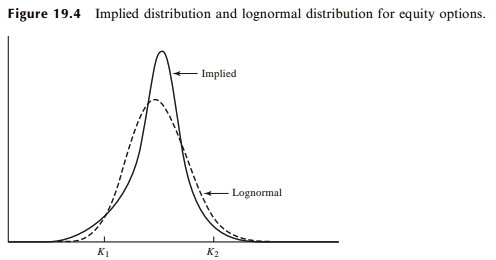
For equities, the fat tail is mostly on the left side as investors tend to react especially strongly when the market is strongly bearish (also called crashophobia).

Volatility term structure

It’s the implied volatility plotted against the maturity.

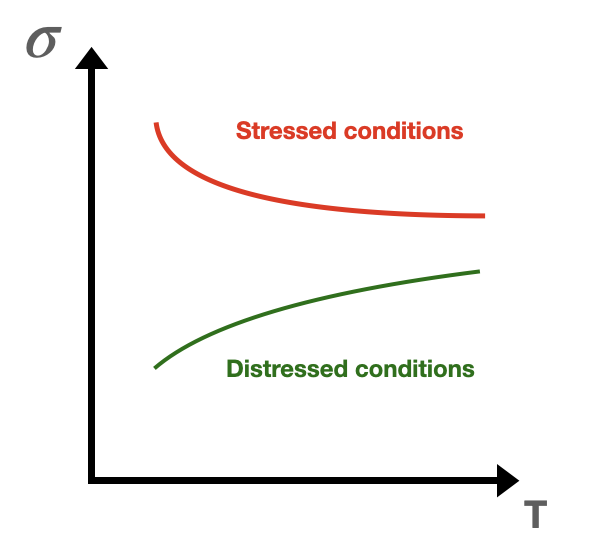
In stressed conditions, the traders are expecting a high short-term volatility.

Volatility surface

It’s the implied volatility plotted against the strike and the maturity.