Assumptions
Preamble: errors are the deviations of the observations from the population, while residuals are the deviations of the observations from the sample.
$Y^{population}_i = \alpha + \beta X^{population}_i + \epsilon_i$ –> $\epsilon_i$ are the errors.
$\hat Y^{sample}_i = \hat \alpha + \hat \beta X^{sample}_i + \hat \epsilon_i$ –> $\hat \epsilon_i$ are the residuals.
The assumptions behind the classical linear regression (OLS - Ordinary Least Squares) model are:
- The variance of errors is constant (homoscedasticity): $\mathbb{V}[\epsilon] = \sigma$. Note: homoscedasticity doesn’t say anything about the correlation between predictors, nor between errors, nor between errors and predictors.
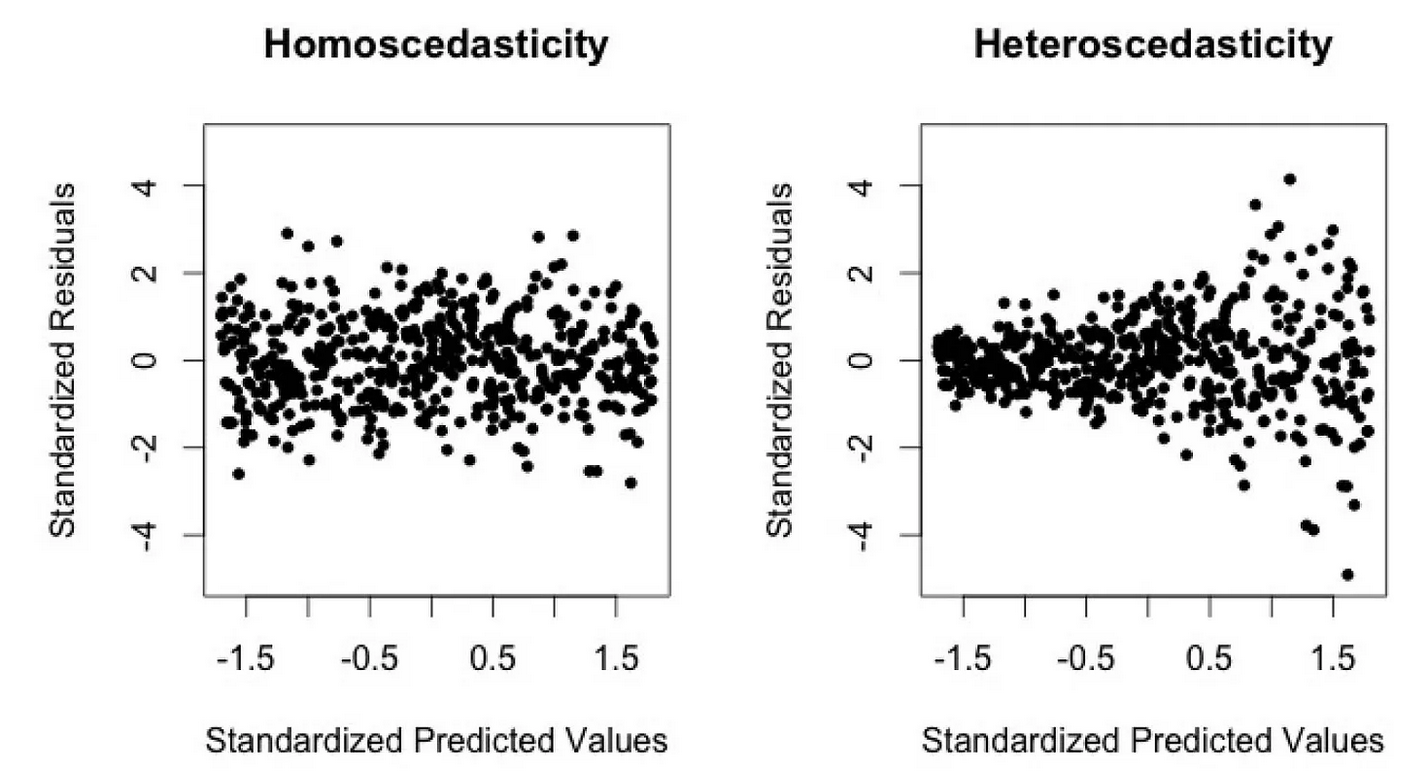
Without homoscedasticity, the estimator becomes unstable (high variance i.e. very sensitive to data). To identify homoscedasticity, one can run through statistical tests such as the White test. Another possibility is to plot the independent variables against the dependent variable (cf figure); if there is a trend, then there is no homoscedasticity.
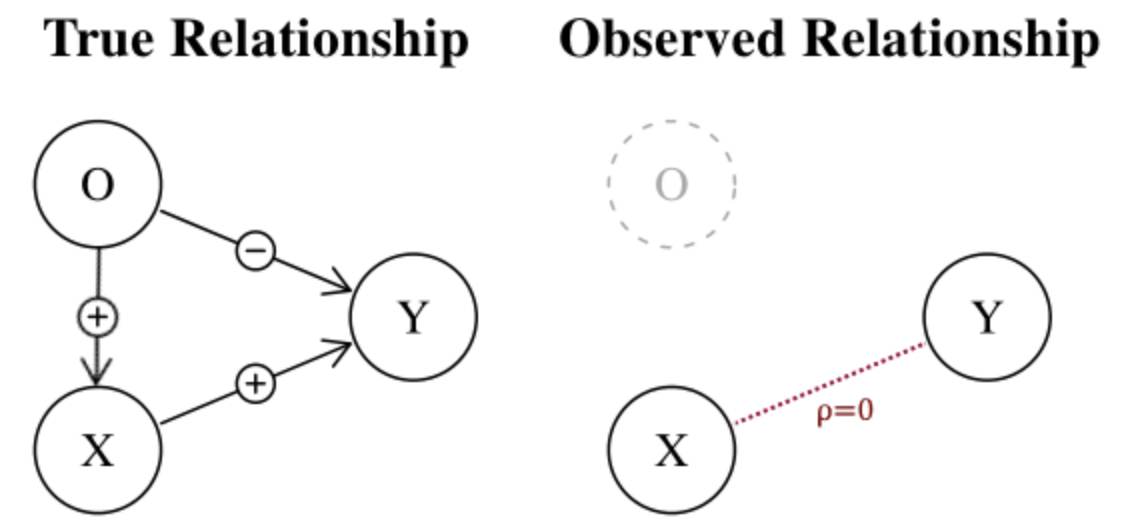
- The errors have conditional mean of zero (exogeneity): $\mathbb{E}[\epsilon | X] = 0$. This means that the errors do not depend on $X$. This assumption is needed to make sure there is no important variable missing that may also explain the relationship. Indeed, if one independent variable is missing, it’s likely that this variable is correlated with the other independent variables as well as the dependent variable. As a result, it is correlated with the errors (since the errors contain everything that is not included in $\alpha + \beta X$). This post and this post highlight the bias when such assumption is not satisfied.
An intuitive example would be trying to predict a company stock price at time $t$ without any indication on the price level before. The bias is clearly seen in the left graph below.

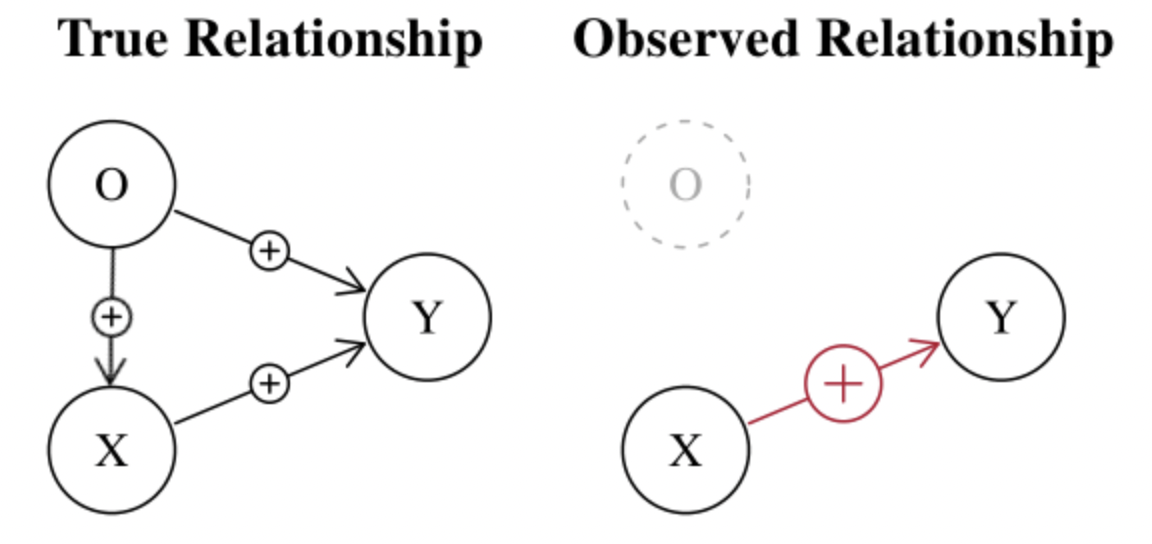
Depending on the sign of influence of the independent variables on the dependent variable, the omitted variable can also hide the relationship:
Example: associated notebook.
Omitted variable bias can also cause spurious correlations i.e. finding cause when there is actually none. In that case the omitted variable is called confounding variable:
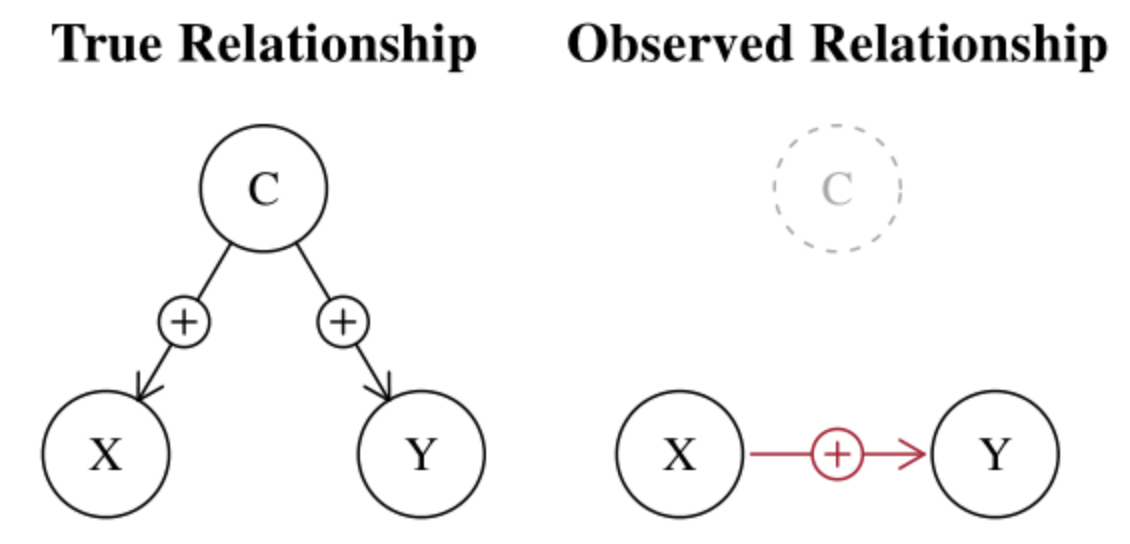
Typical example: Y = ice cream sales; X = swimming suit sales; C = weather.
To detect omitted variables and if all variables are available, we can try out several combinations of independent variables. If the coefficients change, there is an omitted variable.
- The errors are uncorrelated $\mathbb{E}[\epsilon_i \epsilon_j] = 0$. When errors are autocorrelated, the estimator is still unbiased but not with minimal variance. The tests to detect autocorrelation of errors are Durbin-Watson or Ljung-Box. To correct for this problem, one would need to try to include other variables or do some transformations (see $AR(k)$ processes).
Additional assumptions are also sometimes necessary:
-
The explanatory variables are linearly independent. In other words, this means that the matrix $X$ has full rank. If this is not the case, the variance becomes unstable (see “Bias and variance-covariance” section below).
-
The errors are normally distributed.
If the first three assumptions are satisfied, under the Gauss-Markov theorem the OLS estimator is said BLUE (Best Linear Unbiased Estimator). It is unbiased and is has the lowest variance. When the assumptions are violated, it may be better to use the Generalized Least Squares (GLS) or the Weighted Least Squares (WLS) which is a special case of the GLS.
\[\widehat \theta_{OLS} = (X^TX)^{-1}X^TY\] \[\widehat \theta_{GLS} = (X^T\Omega_\epsilon^{-1}X)^{-1}X^T\Omega_\epsilon^{-1}Y\] \[\text{where } \Omega_\epsilon = \mathbb{E}[\epsilon_i \epsilon_j] \text{ i.e. the matrix variance-covariance of the errors}\]Note: LinearRegression from scikit-learn does OLS.
R2
\[R^2 = 1-\frac{\sum (y_i - \hat y_i)^2}{\sum (y_i - \overline y)^2}\]Or:
\[R^2 = \frac{\sum (y_i - \overline y)^2 - \sum (y_i - \hat y_i)^2}{\sum (y_i - \overline y)^2} = \frac{\text{variance explained by the regression}}{\text{variance of }y}\]Problems with $R2$:
- $R2$ tends to drop when the variance is high. However, even if the variance is high, there can still be a strong linear relationship between the data.
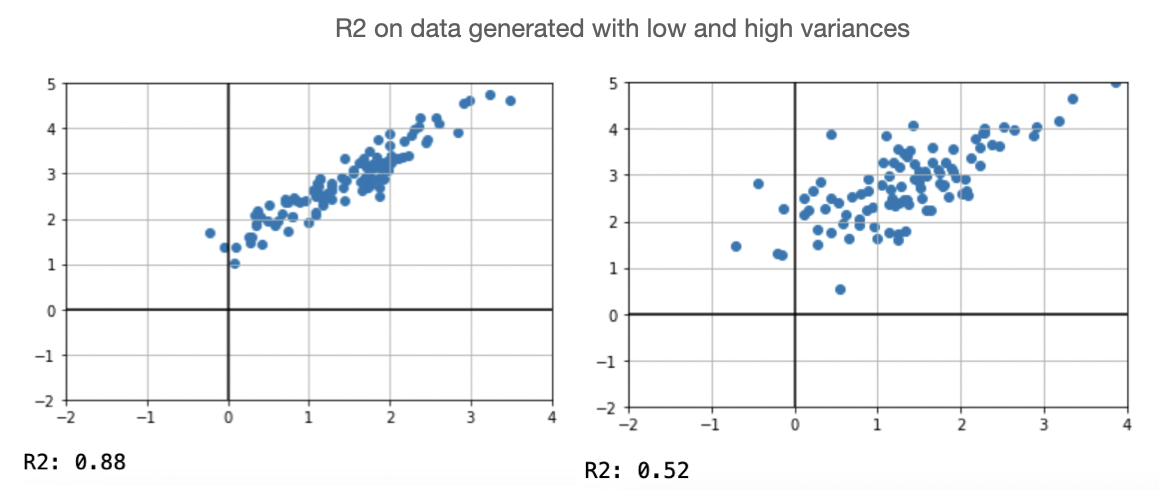
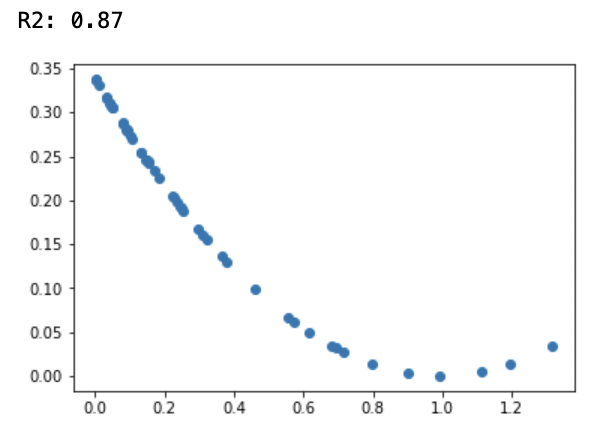
- More generally, high $R2$ is not necessarily good and low $R2$ is not necessarily bad. Below is an example where $R2$ is very high for a non-linear relationship.
Bias and variance-covariance
Hypothesis: \(\begin{cases} \mathbb{E}[\epsilon] = 0 \\ \mathbb{V}[\epsilon] = \sigma \end{cases}\)
Bias
\[Bias = \mathbb{E}[\widehat{\theta}-\theta^*]\] \[\begin{align*} \mathbb{E}[\widehat{\theta}] &= \mathbb{E}[(X^TX)^{-1}X^TY] \\ &= \mathbb{E}[(X^TX)^{-1}X^T(X \theta^* + \epsilon)] \\ &= \theta^* + (X^TX)^{-1}X^T\mathbb{E}[\epsilon] \\ &= \theta^* \end{align*}\]The estimator is not biased.
Variance-covariance
\[\begin{align*} Cov(\widehat{\theta}) &= \mathbb{V}[(X^TX)^{-1}X^TY] \\ &= \mathbb{V}[(X^TX)^{-1}X^T(X \theta^* + \epsilon)] \\ &= 0 + ((X^TX)^{-1}X^T)^T\mathbb{V}[\epsilon] (X^TX)^{-1}X^T \\ &= (X^TX)^{-1}\sigma^2 ~~~~\text{ since $X^TX$ is symmetric} \end{align*}\]Note: the variance-covariance is a matrix. We define here the variance as a number.
$\mathbb{V}[\widehat{\theta}] = \mathbb{E}[(\widehat{\theta} - \mathbb{E}[\widehat{\theta}])^2]$
We know that $||u||_2 = \Sigma_k u_k^2 = Tr(u u^T)$.
Thus:
\[\begin{align*} \mathbb{V}[\widehat{\theta}] &= \mathbb{E}[Tr((\widehat{\theta} - \mathbb{E}[\widehat{\theta}])(\widehat{\theta} - \mathbb{E}[\widehat{\theta}])^T)] \\ &= Tr(\mathbb{E}[(\widehat{\theta} - \mathbb{E}[\widehat{\theta}])(\widehat{\theta} - \mathbb{E}[\widehat{\theta}])^T)] ~~~ \text{ since the trace is a number} \\ &= Tr(Cov(\widehat{\theta})) \\ &= Tr((X^TX)^{-1}\sigma^2) \\ &= \sigma^2Tr((UDU^T)^{-1}) ~~~ \text{ thanks to the spectral theorem (we assume inversible matrices)} \\ &= \sigma^2Tr((UU^T)^{-1}D^{-1}) ~~~ \text{ thanks to the trace properties} \\ &= \sigma^2Tr(D^{-1}) ~~~ \text{ since $U$ is orthogonal} \\ &= \sigma^2Tr(\begin{bmatrix}\frac{1}{\lambda_1} & \dots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \dots & \frac{1}{\lambda_p}\end{bmatrix})~~~ \text{with $\lambda_i$ the eigenvalues} \\ &= \sigma^2\Sigma_{k=1}^p \frac{1}{\lambda_k} \end{align*}\]We can see that the variance becomes unstable when eigenvalues are small, which is the case when variables are collinear.