Variance

Variance theoretical formula: $\mathbb{V}[X] = \mathbb{E}[(X-\mathbb{E}[X])^2]$

Variance empirical formula: $var_n(x) = \frac{1}{n} \sum_{i=1}^n (x_i - \bar x)^2$

Variance (sample) empirical formula: $var_n(x) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2$

The sample variance is larger than the population variance so that it takes into account of additional uncertainty .

Volatility

Volatility empirical formula: $\sigma = \sqrt{var_n(x)}$

The volatility is most often computed from the returns. Intuitively, it represents the “typical variation around the mean”.

If the variable is normally distributed, the below figure is important to have an order of magnitude:

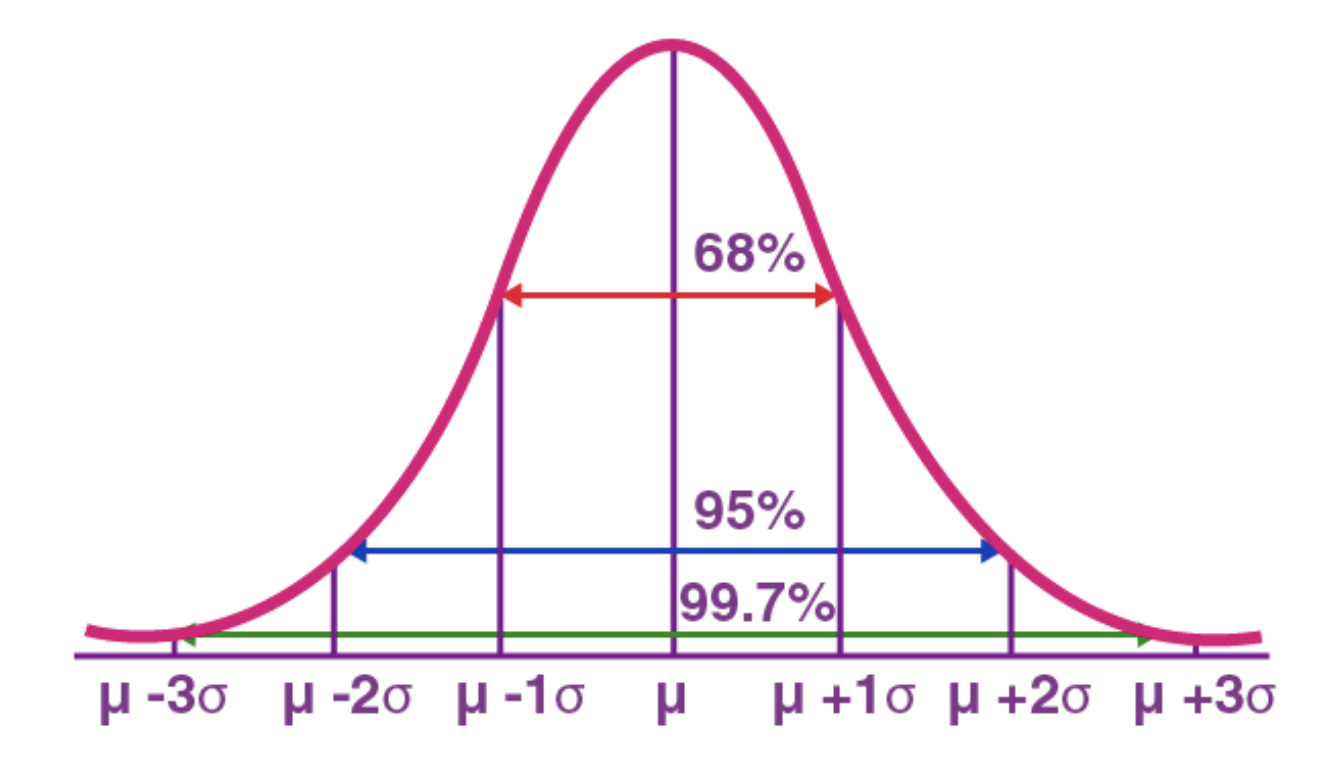
Volatility is important in algorithmic trading since a good trade should be profitable after fees deduction. Hence the asset move should be large enough to pay the fees.

Note: the mean of absolute returns (MAR) can be more relevant in some cases as it reflects the typical variation. The standard deviation is often used as it penalizes more the big moves. E.g. a stock that does [-1%,1%,-10%,1%] would have MAR=3.3% and STD=4.6%. Also, the STD is about the deviation around the mean: [-1%,-1%,-1%,-1%] would give MAR=1% but STD=0% (the stock does not move around the mean). Moreover, the standard deviation has nice statistical properties e.g. it is used in the central limit theorem.

Variance of a portfolio

Let’s find the formula starting with a small portfolio with number of assets = 2.

\[R_p = \omega_1 R_1 + \omega_2 R_2\] \[\begin{align*} \mathbb{V}[R_p] &= \mathbb{V}[\omega_1 R_1 + \omega_2 R_2] \\ &= \omega_1^2\mathbb{V}[R_1]+\omega_2^2\mathbb{V}[R_2]+2\omega_1\omega_2Cov(R_1,R_2) \quad \quad \quad (*)\\ &= (\omega_1~~\omega_2) \begin{pmatrix} \mathbb{V}[R_1] & Cov(R_1, R_2) \\ Cov(R_1, R_2) & \mathbb{V}[R_2] \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} \\ \end{align*}\]

We can thus generalize the formula:

\[\sigma_p^2= \omega^T \Sigma \omega\]

$(*)$ can also be written using the correlation coefficient $\rho$:

$\mathbb{V}[R_p] = \omega_1^2\mathbb{V}[ R_1]+\omega_2^2\mathbb{V}[R_2]+2\omega_1\omega_2 \sqrt{\mathbb{V}[ R_1]} \sqrt{\mathbb{V}[ R_2]} \rho_{1,2}$

From this equation, we can see that the portfolio variance is maximized when $\rho_{ij}=1$ (perfect correlation). It is minimal when $\rho_{ij}=-1$ i.e. when assets are perfectly negatively correlated. We notice than when $\rho_{ij}=1$, we have $\mathbb{V}[R_p] = (\omega_1\sigma_1 + \omega_2\sigma_2)^2$. This result shows that when assets are perfectly correlated, the volatility of a portfolio is the weighted average of the assets’ volatilities.

We could also compute the portfolio volatility using the correlation matrix. This is useful for better interpretation (it’s easier to double check a correlation matrix than a covariance matrix).

\[\sigma^2_p = \omega^T S C S \omega\]

where $C$ is the correlation matrix and $S$ the standard deviation (diagonal) matrix:

\[S = \begin{pmatrix} \sigma_1 & \\ & \ddots & \\ & & \sigma_n \end{pmatrix}\]

Warning: make sure the standard deviations and not the variances are used in $S$. It’s also important to make sure those standard deviations are of the right unit (e.g. annualized).

Annualization

Annualize refers to converting a short-term number, such as an investment return or interest rate, into an annual rate.

Note:

• annual volatility: computed on several years e.g. 2020, 2021, 2022.

• annualized volatility: computed on one year based on monthly or daily returns.

In practice, we use the annualized volatility because we don’t have the annual returns of a large sample of years.

Let us say we want to compute the annualized standard deviation based on the monthly returns. When returns are continuous:

\[\begin{align*} var(r_{2020}) &= var(r_{jan, 2020}+...+r_{dec, 2020}) \quad \text{Reminder: when returns are continuous: } r_{0,2} = r_{0,1}+r_{1,2}\\ &= var(\sum_{i=1}^{12}r_{i, 2020}) \\ &= \sum_{i=1}^{12}var(r_{i, 2020}) \quad \text{assuming independent returns}\\ &= 12var(r_{monthly}) \\ \end{align*}\]

Thus, we have:

\[\sigma_{annualized} = \sqrt{12}\sigma_{monthly}\]

Similarly, assuming trading happens all day long:

\[\sigma_{annualized} = \sqrt{365 * var_{daily}(x)} = \sqrt{365} \sigma_{daily}\]

Examples

• VIX: 15-20% (typical level in normal market environment).

Note: the VIX is a measure of the expected equity volatility.

• BTCUSD: 20% monthly (2019).

• BTCUSD: 84% annualized daily (2021).

• BTCUSD: 0.53% hourly (October 2022).

• XRPUSD: 1.17% hourly (October 2022).

Risk contribution in portfolio volatility

The risk contribution helps to quantify the impact of an asset on the portfolio volatility. It considers 3 elements:

• the asset’s volatility

• the asset’s weight

• the asset’s correlation with other assets

\[\text{marginal contribution} = \frac{\partial \sigma_p}{\partial \omega}\]

The marginal contribution is by how much the portfolio variance changes if we slightly increase one holding. For more clarity, we can use the following relationship:

\[\Delta \sigma_p = \frac{\partial \sigma_p}{\partial \omega} \Delta \omega\]

Numerical example:

$\sigma_p^{(1)} = 8.3\%$

$\frac{\partial \sigma_p}{\partial \omega} = 7.8\%$

$\omega_1^{(1)} = 33\%$

If $\omega_1^{(2)} = 83\%$, then $\Delta \sigma_p = 7.8\% * (83\%-33\%) = 3.9\%$.

Thus, $\sigma_p^{(2)} = \sigma_p^{(1)} + \Delta \sigma_p \approx 12.1\%$.

Derivation:

$\frac{\partial \sigma_p}{\partial \omega} = \frac{\partial \sqrt{\omega^T \Sigma \omega}}{\partial \omega}$

We know that: $(\sqrt u)’ = \frac{u’}{2 \sqrt{u}}$

Say there are 3 assets,

\[\begin{align*} x^TAx &= ... \\ &= x_1^2a_{11} + x_1x_2(a_{12}+a_{21}) + x_2^2 a_{22} + x_1x_3(a_{13}+ a_{31}) + x_3^2a_{33} + x_2x_3(a_{23}+a_{32}) \\ &= x_1^2a_{11} + x_2^2 a_{22} + x_3^2a_{33} + 2x_1x_2cov_{1,2} + 2x_1x_3cov_{1,3} + 2x_2x_3cov_{2,3} \\ & (\text{because } A \text{ is symmetric (}a_{ij}=a_{ji}\text{)}) \\ \end{align*}\]

$\frac{\partial \sigma_p}{\partial x_1} = 2x_1a_{11} + 2x_2cov_{1,2} + 2x_3 cov_{1,3}$

In general, $\frac{\partial \sigma_p}{\partial x_k} = 2 \sum_{i=1}^n x_i a_{k_i} = 2Ax$

Hence,

\[\frac{\partial \omega^T \Sigma \omega}{\partial \omega} = 2 \Sigma \omega\]

Finally,

\[\frac{\partial \sqrt{\omega^T \Sigma \omega}}{\partial \omega} = \frac{2 \Sigma \omega}{2 \sqrt{\omega^T \Sigma \omega}} = \frac{1}{\sigma_p} \Sigma \omega\]

Note: $\frac{1}{\sigma_p} \Sigma \omega$ is a vector where each component is the risk contribution of the holding.

One can also weight the risk contributions:

\[\omega \odot \frac{1}{\sigma_p} \Sigma \omega\]

That way, when we sum over the vector’s components, \(\sum_i \big( \omega \odot \frac{1}{\sigma_p} \Sigma \omega \big)_i = \sigma_p\)

In general, one asset would strongly contribute to the portfolio volatility if one of the following statement is true:

• it has a high weight

• it has a high volatility

• it is highly correlated to other assets with a high volatility

See this notebook for examples with synthetic data.