An integral is classically defined as the area under the curve. Integrals are heavily used in finance since $\text{price} = \text{weighted average of all possible outcomes} = \text{expected value} = \text{integral (in continuous time)}$. Or, put it differently: $\text{payoff} = \text{accumulated gains} = \text{area under the curve} = \text{integral}$.
From Wikipedia: “The integrand is how much stock we hold, the integrator represents the movement of the prices, and the integral is how much money we have in total including what our stock is worth, at any given moment. The prices of stocks and other traded financial assets can be modeled by stochastic processes such as Brownian motion or, more often, geometric Brownian motion (see Black–Scholes).”

Riemann integrals
Definition
Integrals that are deterministic can be approximated using the Riemann sum (good tutorial) that uses a finite sum:
\[Area \approx \sum_{k=1}^n f(x_k) \Delta x\]With $n$ the number of rectangles considered.
\[n \uparrow~=>~ \Delta x \downarrow ~=>~error \downarrow\]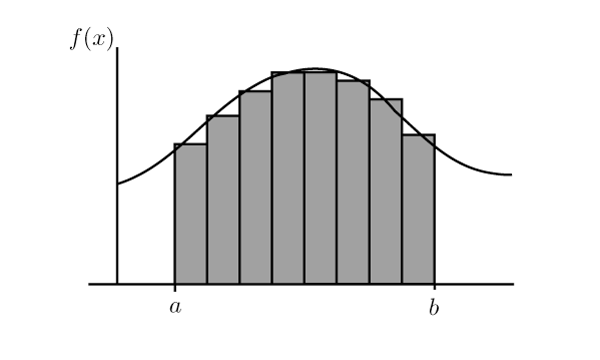
Exact value
Given a function $f$ that is continuous on the interval [a,b] we divide the interval into $n$ subintervals of equal width, $\Delta x$, and from each interval choose a point, $x_k$. Then the definite integral of $f(x)$ from $a$ to $b$ is:
\[Area = \int_a^b f(x) dx = lim_{n \to \infty}\sum_{k=1}^n f(x_k) \Delta x\]Itô integrals
Itô integrals are adapted for processes involving a random component.
A Wiener process can’t be integrated using a Riemann sum since it has infinite (i.e. unbounded) variations. Indeed, as time increases, the volatility increases too, hence prices tend to show unpredictable variations that can’t be bounded.
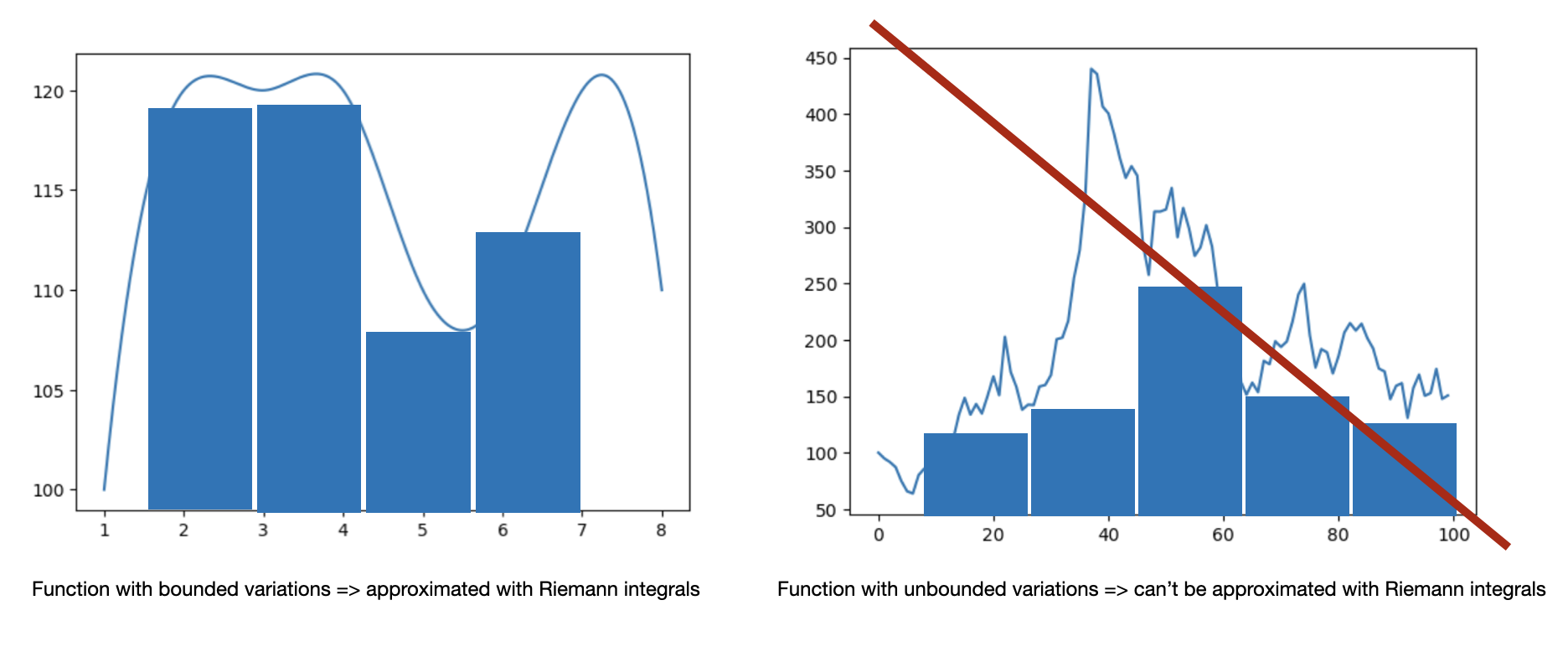

To cope with this issue, the Itô calculus is based on an integral that requires the integrand only to be square integrable. The Itô integral is then defined based on a quadratic convergence:

Note: a function $f$ is square-integrable if $\int_0^t f_u^2 du < \infty$. This characteristic is useful to make sure the fluctuations (variance = second moment) are not exploding when increasing the range of values. We say that the integral “converge” i.e. the sum or the area is not infinite when we consider a wider range of values.