Dynamic Programming

In the context of trading, dynamic programming can be used to learn the optimal strategy.

As explained in the Intro to Reinforcement Learning, the value function is the expected gain at each step:

\[V_\pi(s_t) = \mathbb{E}_\pi[R_0 + \gamma V_\pi(s_{t+1}) | s_0 = s_t]\]

The actions are buy/hold/sell and the rewards are the profits made with specific actions.

The optimal strategy are the actions that maximize the gains at each steps.

Example

We assume the following:

all prices are known at all times
we can’t go short

What’s the best strategy to buy/sell?

In this case, $\gamma = 1$ since all prices are all known in advance.

import numpy as np

import matplotlib.pyplot as plt

ret_ann = .1
sigma_ann = .1

n = 30

np.random.seed(3)
single_returns = np.random.normal(ret_ann/12, sigma_ann/np.sqrt(12), n)

ret_cumul = (1+single_returns).cumprod()-1

prices = 100*(1+ret_cumul)

def bellman_actions(prices):
    n = len(prices)

    # reward = profit
    # state = hold the asset or not
    
    # Initialize a 2D table for memoization
    # rewards[i][state] represents the maximum profit (reward) that can be made at time t for a given state
    rewards_profits = [[0 for _ in range(2)] for _ in range(n)]

    # Initialize a 2D table to store the actions
    # actions[i][state] represents the action that leads to the maximum profit (reward) at time t for a given state
    actions = [['-' for _ in range(2)] for _ in range(n)]

    # On the last day, if we are not holding any asset, the profit is 0
    # If we're holding the asset, we have to sell it, so the profit is the price on the last day
    rewards_profits[n - 1][0] = 0
    rewards_profits[n - 1][1] = prices[n - 1]

    # For each time step t and for each holding state, 
    # we compute the maximum profit and the corresponding action 
    # we go backward
    for t in range(n - 2, -1, -1): 
        for state_holding in range(2):
            if state_holding == 0:
                # If we are not holding the asset, we can either buy or do nothing
                # The maximum profit (reward) is the maximum of these two choices
                reward_buy = -prices[t] + rewards_profits[t + 1][1]
                reward_hold = rewards_profits[t + 1][0]
                rewards_profits[t][state_holding] = max(reward_buy, reward_hold)
                if rewards_profits[t][state_holding] == reward_buy:
                    # If buying leads to the maximum profit, the action is 'BUY'
                    actions[t][state_holding] = 'buy'
            else:
                # If we are holding the asset we can either sell or do nothing
                # The maximum profit is the maximum of these two choices
                reward_sell = prices[t] + rewards_profits[t + 1][0]
                reward_hold = rewards_profits[t + 1][1]
                rewards_profits[t][state_holding] = max(reward_sell, reward_hold)
                if rewards_profits[t][state_holding] == reward_sell:
                    # If selling leads to the maximum profit, the action is 'SELL'
                    actions[t][state_holding] = 'sell'

    # Start from day 0, no asset is held
    t = 0
    state_holding = 0
    action_list = []
    while t < n:
        # Append the action for the current state
        action_list.append(actions[t][state_holding])
        if actions[t][state_holding] == 'buy':
            # If the action is 'BUY', change the holding state to 1
            state_holding = 1
        elif actions[t][state_holding] == 'sell':
            # If the action is 'SELL', change the holding state to 0
            state_holding = 0
        t += 1

    return action_list

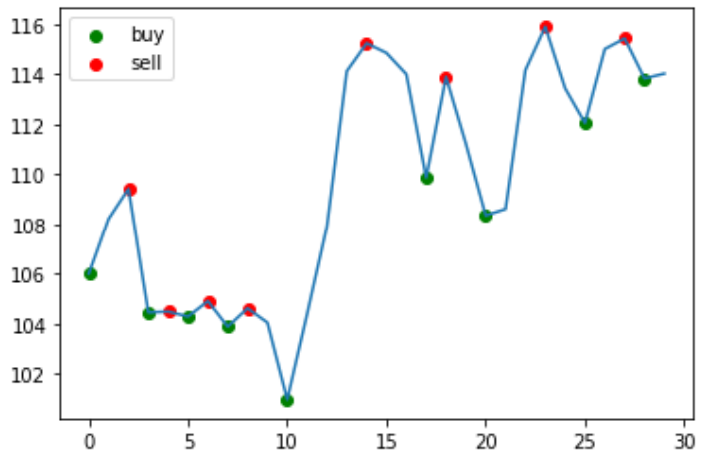
actions = bellman_actions(prices)

idx_buy = [i for i, action in enumerate(actions) if action=='buy']
value_buy = [prices[i] for i, action in enumerate(actions) if action=='buy']

idx_sell = [i for i, action in enumerate(actions) if action=='sell']
value_sell = [prices[i] for i, action in enumerate(actions) if action=='sell']

plt.plot(prices)
plt.scatter(idx_buy, value_buy, color='g', label='buy')
plt.scatter(idx_sell, value_sell, color='r', label='sell')
plt.legend()
plt.plot()

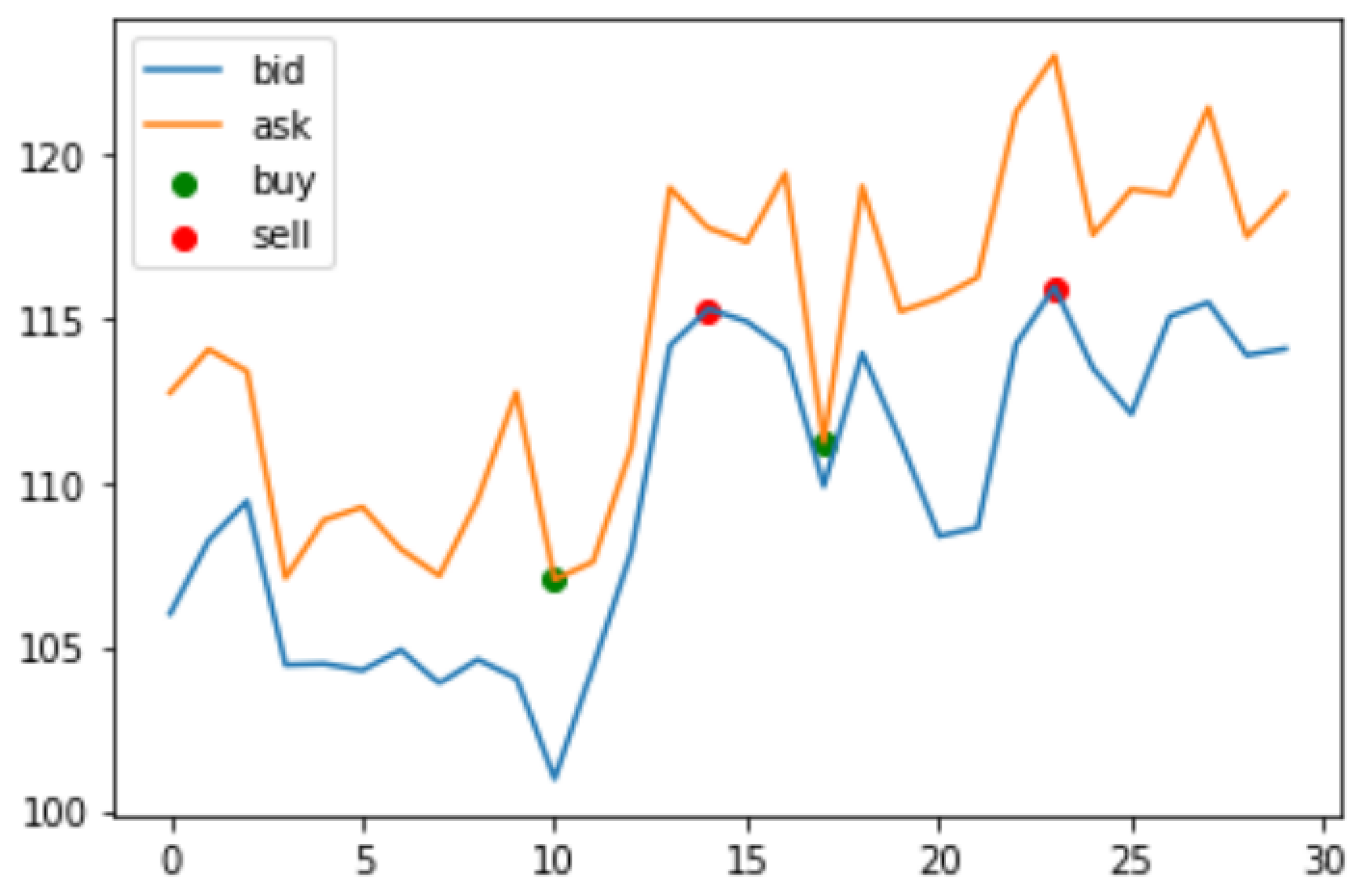
# BELLMAN WITH BID-ASK

import numpy as np
import matplotlib.pyplot as plt

ret_ann = .1
sigma_ann = .1

n = 30

np.random.seed(3)
single_returns = np.random.normal(ret_ann/12, sigma_ann/np.sqrt(12), n)

ret_cumul = (1+single_returns).cumprod()-1

bid_prices = 100*(1+ret_cumul)
ask_prices = bid_prices + np.random.uniform(.5,10,n)

def bellman_actions(ask, bid):
    n = len(ask)

    # reward = profit
    # state = hold the asset or not
    
    # Initialize a 2D table for memoization
    # rewards[i][state] represents the maximum profit (reward) that can be made at time t for a given state
    rewards_profits = [[0 for _ in range(2)] for _ in range(n)]

    # Initialize a 2D table to store the actions
    # actions[i][state] represents the action that leads to the maximum profit (reward) at time t for a given state
    actions = [['-' for _ in range(2)] for _ in range(n)]

    # On the last day, if we are not holding any asset, the profit is 0
    # If we're holding the asset, we have to sell it, so the profit is the price on the last day
    rewards_profits[n - 1][0] = 0
    rewards_profits[n - 1][1] = bid[n - 1]

    # For each time step t and for each holding state, 
    # we compute the maximum profit and the corresponding action 
    # we go backward
    for t in range(n - 2, -1, -1): 
        for state_holding in range(2):
            if state_holding == 0:
                # If we are not holding the asset, we can either buy or do nothing
                # The maximum profit (reward) is the maximum of these two choices
                reward_buy = -ask[t] + rewards_profits[t + 1][1]
                reward_hold = rewards_profits[t + 1][0]
                rewards_profits[t][state_holding] = max(reward_buy, reward_hold)
                if rewards_profits[t][state_holding] == reward_buy:
                    # If buying leads to the maximum profit, the action is 'BUY'
                    actions[t][state_holding] = 'buy'
            else:
                # If we are holding the asset we can either sell or do nothing
                # The maximum profit is the maximum of these two choices
                reward_sell = bid[t] + rewards_profits[t + 1][0]
                reward_hold = rewards_profits[t + 1][1]
                rewards_profits[t][state_holding] = max(reward_sell, reward_hold)
                if rewards_profits[t][state_holding] == reward_sell:
                    # If selling leads to the maximum profit, the action is 'SELL'
                    actions[t][state_holding] = 'sell'

    # Start from day 0, no asset is held
    t = 0
    state_holding = 0
    action_list = []
    while t < n:
        # Append the action for the current state
        action_list.append(actions[t][state_holding])
        if actions[t][state_holding] == 'buy':
            # If the action is 'BUY', change the holding state to 1
            state_holding = 1
        elif actions[t][state_holding] == 'sell':
            # If the action is 'SELL', change the holding state to 0
            state_holding = 0
        t += 1

    return action_list

actions = bellman_actions(ask_prices, bid_prices)

idx_buy = [i for i, action in enumerate(actions) if action=='buy']
value_buy = [ask_prices[i] for i, action in enumerate(actions) if action=='buy']

idx_sell = [i for i, action in enumerate(actions) if action=='sell']
value_sell = [bid_prices[i] for i, action in enumerate(actions) if action=='sell']

plt.plot(bid_prices, label='bid')
plt.plot(ask_prices, label='ask')
plt.scatter(idx_buy, value_buy, color='g', label='buy')
plt.scatter(idx_sell, value_sell, color='r', label='sell')
plt.legend()
plt.plot()