The Naive Bayes classifier is a Bayes classifier that assumes independence of features (naive).

It is entirely based on the Bayes formula:

\[\mathbb{P}(\theta | X) = \frac{\mathbb{P}(\theta)\mathbb{P}(X | \theta)}{\mathbb{P}(X)}\]

where: $\theta$ = class or label (= parameter)

In practice, we don’t compute the denominator term that does not depend on the class and more used as a normalization term:

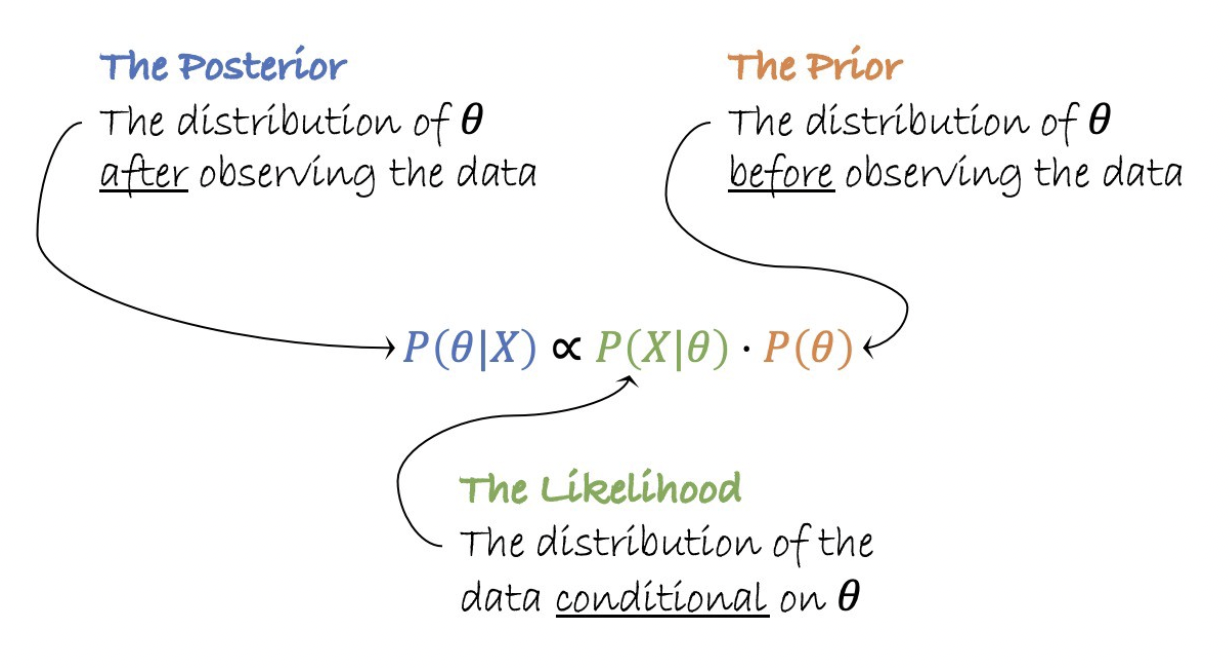
To classify, we need to find the class that maximizes the posterior probability.

Example (spam detector):

hello you -> spam

absence -> no spam

you lost -> spam

meeting late -> no spam

“my meeting” –> spam?

Let us define the following variables:

• $\text{count}(w)_{\theta=c}$ is the count of a word for a specific class.

• $N_{\theta=c}$ is the number of words belonging to a specific class in the whole corpus (training set).

• $N$ is the number of words in the whole corpus.

$\theta$ = spam

\[\begin{align*} \text{prior} &= \mathbb{P}(\theta = \text{spam}) \\ &= \frac{N_{\theta = \text{spam}}}{N} \\ &= \frac{4}{7} \end{align*}\] \[\begin{align*} \text{likelihood} &= \mathbb{P}(X = "my~meeting" | \theta = \text{spam}) \\ &= \prod_{w \in "my~meeting"} \frac{\text{count}(w)_{\theta=\text{spam}}+1}{N_{\theta=\text{spam}} +N} \\ &= \frac{0+1}{4+7}\frac{0+1}{4+7} \\ &= \frac{1}{121} \end{align*}\]

Thus:

\[\begin{align*} \text{posterior} &= \mathbb{P}(\theta = \text{spam} | X = "my~meeting") \\ &\propto \mathbb{P}(\theta = \text{spam})\mathbb{P}(X = "my~meeting" | \theta = \text{spam}) \\ &= \frac{4}{7}\frac{1}{121} \\ &\approx 0.00471 \end{align*}\]

$\theta$ = no spam

\[\begin{align*} \text{prior} &= \mathbb{P}(\theta = \text{no spam}) \\ &= \frac{N_{\theta = \text{no spam}}}{N} \\ &= \frac{3}{7} \end{align*}\] \[\begin{align*} \text{likelihood} &= \mathbb{P}(X = "my~meeting" | \theta = \text{no spam}) \\ &= \prod_{w \in "my~meeting"} \frac{\text{count}(w)_{\theta=\text{no spam}}+1}{N_{\theta=\text{no spam}} +N} \\ &= \frac{0+1}{4+7}\frac{1+1}{4+7} \\ &= \frac{2}{121} \end{align*}\]

Thus:

\[\begin{align*} \text{posterior} &= \mathbb{P}(\theta = \text{no spam} | X = "my~meeting") \\ &\propto \mathbb{P}(\theta = \text{no spam})\mathbb{P}(X = "my~meeting" | \theta = \text{no spam}) \\ &= \frac{3}{7}\frac{2}{121} \\ &\approx 0.00712 \end{align*}\]

$\theta = \text{no spam}$ maximizes the posterior probability.

Note: we use $+1$ and $+N$ in the likelihood since we don’t want probabilities for words we haven’t seen to be zero, otherwise they will set the whole product in the likelihood to be zero. See additive smoothing.

The Naive Bayes classifier is often used as a benchmark because it’s a simple classifier to compute and it gives good results.