DBSCAN (Density-Based Spatial Clustering of Applications with Noise) is an algorithm allowing to find clusters based on a density and classication of points.

Note: density can be seen as the number of points in one’s neighborhood.

The algorithm has two main parameters:

• $\epsilon$ is the size of the neighborhood.

• $MinPts$ is the minimum points in $\epsilon$-neighborhood to define a cluster.

Every point is classified among three categories:

• A core point has at least $MinPts$ points in its $\epsilon$-neighborhood.

• A border point has less than $MinPts$ points in its neighborhood but at least one core point is present.

• An outlier is neither a core nor a border point.

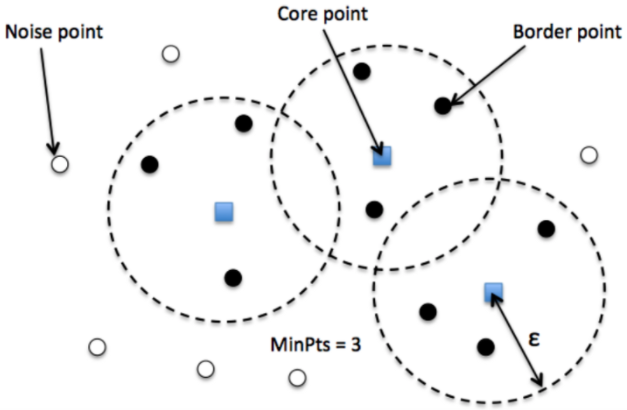
DBSCAN uses density-reachability to navigate through points and identify clusters.

Density-reachability: a point $y$ is density-reachable from $x$ if there is a path $p_1,…, p_n$ with $p_1=x$ and $p_n=y$ where each $p_{i+1}$ on the path must be core points with the possible exception of $p_n$. To find density-reachable neighbors, we find all neighbors of a point and repeat the process with the last found neighbors (i.e. find neighbors of neighbors) until there are not enough points in the neighborood of a point.

Its main advantages over k-means is that it can find non convex clusters as well as detecting outliers (noise).

Parameter estimation

High $MinPts$ or low $\epsilon$ means higher density is necessary to form a cluster.

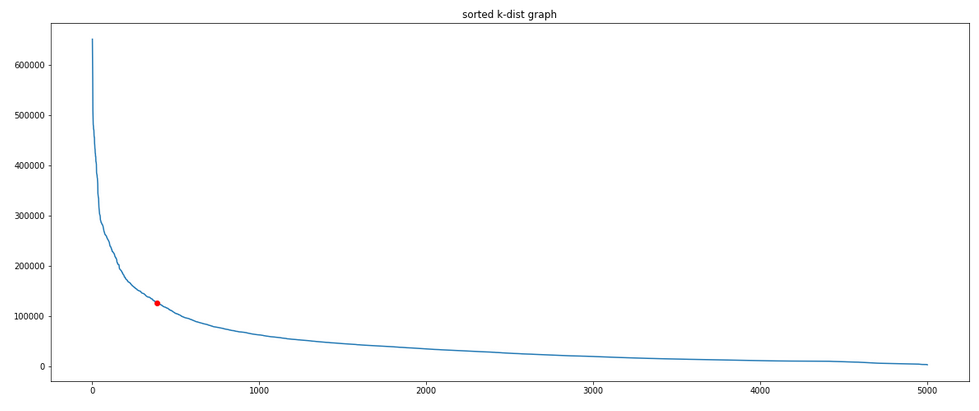
The original DBSCAN paper proposes a method to define $\epsilon$. The method consists in plotting the k-th distance to each point in decreasing order. The k-th distance is the distance to the furthest point in the neighborhood of a core point, k being equal to $MinPts$ (see above). In other words, it measures how compact is the neighborhood of a point within a cluster (core point). The largest values (left of the graph) are associated with outliers; smaller values are associated with cluster points. The inflection point is the cluster point with the highest k-distance; it corresponds to the epsilon we are looking for.

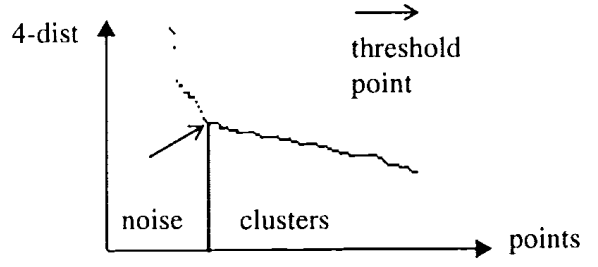
The authors mention that finding the threshold point automatically is rather difficult. They suggest that the user has to estimate the percentage of noise. I propose the following method to determine the threshold dynamically:

• Compute the slope of the line that links the first and last point in the graph.

• Find the two successive points with the closest slope.

The threshold will be the first of the two found points.

Implementation

class MyDBSCAN():
    
    def __init__(self, min_pts=3, eps=.3):
        self.min_pts = min_pts
        self.eps = eps
        self.dict_cluster = {}
    
    def neigh_eps(self, x_point, points, eps):
        dist = np.linalg.norm(x_point-points, axis=1)
        return list(np.where(dist<=eps)[0])
    
    def expand_cluster(self, points, idx_point, idx_neigh, cluster_id, idx_points_visited):
        self.dict_cluster[idx_point] = cluster_id
        neigh_mutable = idx_neigh.copy()
        for idx_n in neigh_mutable: # mutable list! it allows to grow the cluster
            if not idx_points_visited[idx_n]:
                idx_points_visited[idx_n] = True
                idx_neigh_neigh = self.neigh_eps(points[idx_n], points, self.eps)
                if len(idx_neigh_neigh)>=self.min_pts:
                    [neigh_mutable.append(i) for i in idx_neigh_neigh if i not in neigh_mutable]
            if idx_n not in self.dict_cluster.keys() or self.dict_cluster[idx_n]==-1:
                self.dict_cluster[idx_n] = cluster_id
        return idx_points_visited
        
    
    def predict_cluster(self, data):
        points = np.array(data)
        idx_points_visited = np.full(len(points), False) # all points are unvisited
        cluster_id = 0
        while(len(np.where(idx_points_visited==False)[0])!=0): # while there is at least one unvisited point
            idx_point = np.where(idx_points_visited==False)[0][0]
            idx_points_visited[idx_point] = True
            idx_neigh = self.neigh_eps(points[idx_point], points, self.eps)
            if len(idx_neigh)<self.min_pts:
                self.dict_cluster[idx_point] = -1 # the point is classified as noise
            else:
                cluster_id += 1
                # go through neighbors of neighbors
                idx_points_visited = self.expand_cluster( 
                               points, 
                               idx_point, 
                               idx_neigh,
                               cluster_id,
                               idx_points_visited)
        od = collections.OrderedDict(sorted(self.dict_cluster.items()))
        return [od[key] for key in od.keys()]

See dbscan-from-scratch.ipynb for a full comparison with scikit-learn.